solución de sistemas lineales por el método de reducción de renglones
Ej: 2x + 3y = 3
x + 2y = 5
puede observarse. [ 2 3 | 3 ]
[ 1 -2 | 5 ]
x + 2y = 5
puede observarse. [ 2 3 | 3 ]
[ 1 -2 | 5 ]
para las variables x,y,z y t en eso orden la matriz aumentada
EJEMPLO #1
[2 -1 3 4 5 ]
1 3 -2 0 7
-4 0 5 1 -3
correspondiente al sistema lineal
EJEMPLO #1
[2 -1 3 4 5 ]
1 3 -2 0 7
-4 0 5 1 -3
correspondiente al sistema lineal
2x - y + 3z + 4t = 5
x+ 3y - 2z + ot = 7
-4y + 0y + 5y + 1t = -3
EJEMPLO 2
reducir el sistema
3x-2y = 4
x+ 3y = 5
solución
[3 -2 /4 ] R1 - R2 [1 3 / 5 ] R2 3R1 [1 3 / 5 ] R2 - 11 [ 1 3 / 5 ]
1 3 / 5 → 3 -2 / 4 → 0 -11 /-11 → 0 1 / 1
→ R1 resta 3vcR2 [ 1 0 / 2 ]
0 1 / 1
sistemas singulares
En general un sistema no tendrá ninguna solución si se obtiene un renglón en que todos los elementos sean cero excepto el último elemento del renglón.
A sí mismo, se dice que un sistema es consistente si al menos se tiene que un sistema o que es inconsistente si no tiene una solución.
Ejemplo:
inversas y determinantes
Cuando se estudian las matrices hay operaciones que son elementales y de fundamental interés:
1. determinantes
Toda matriz A cuadrada de orden n lleva asociado un valor numérico llamado determinante de A y que denotaremos indistintamente por:
│A│ = det(A)
Este número puede tener múltiples significados, y por resaltar alguno, es muy útil en el estudio de aspectos geométricos, como puede ser el cálculo de la ecuación de una recta que pasa por dos puntos.
Existen distintas formas de definir el determinante de una matriz A, si bien para algunos tamaños de la matriz es muy fácil. Así, para una matriz de tamaño 1 o 2, el determinante se obtiene.
Matriz de orden 1
│a11│ = a11
matriz de orden 2
Propiedades de los determinantes.
El uso de determinantes simplifica de forma muy notable la resolución de sistemas de ecuaciones lineales. Para ello, se aplican propiedades generales que permiten acometer la discusión y la resolución de tales sistemas mediante un procedimiento riguroso
En el manejo de determinantes se pueden establecer algunas propiedades que facilitan las operaciones de cálculo. Tales propiedades son:
1. Una matriz cuadrada con una fila o una columna en la que todos los elementos son nulos tiene un determinante igual a cero.
2. El determinante de una matriz con dos filas o dos columnas iguales es nulo.
3. Cuando dos filas o dos columnas de una matriz son proporcionales entre sí (una se puede obtener multiplicando la otra por un factor), su determinante es cero.
4. Al intercambiar dos filas o dos columnas de una matriz, su determinante cambia de signo.
5. Al multiplicar todos los elementos de una fila o una columna de una matriz por un número, el determinante de la matriz resultante es igual al de la original multiplicado por ese mismo número.
6. El determinante de una matriz triangular o una matriz diagonal es igual al producto de los elementos de su diagonal principal.
7. Cuando a una fila (o columna) de una matriz se le suma o resta una combinación lineal de otras filas (o columnas), el valor de su determinante no se altera.
Para el cálculo del determinante de una matriz es conveniente conocer alguna de las propiedades que los caracterizan, las cuales pueden facilitar a veces el cálculo.
1) El determinante de una matriz A es igual al de su traspuesta: Det(A) = Det (A¨t)
1) El determinante de una matriz A es igual al de su traspuesta: Det(A) = Det (A¨t)
2) El determinante de un producto de matrices es igual al producto de sus determinantes:
丨A.B丨=丨A丨.丨B丨.
4) El determinante de la inversa de una matriz es igual al inverso del determinante de la matriz.
丨A"-1丨= __1__
丨A丨
5) La suma de los productos de los elementos de una fila o columna de una matriz por los adjuntos de otra fila o columna es siempre nula.
6) La matriz de los adjuntos de una matriz A dada de dimensión n tiene un determinante igual al determinante de A elevado a n-1.
2. inversas
Este concepto sólo tiene sentido para matrices cuadradas con determinante distinto de cero, como expondremos a continuación. El cálculo de la inversa de una matriz lo utilizaremos en diversos campos, por ejemplo, para encontrar bases en un determinado espacio, o en otro tema totalmente distinto, para calcular la suma de una serie (mediante el cálculo de la inversa de Leontief).
dada una matriz A de orden n si existe una matriz, que notaremos A*-1, que verifica:
A x A*-1 = A*-1 x A = I
se dice que A es invertible y que A-1 es la matriz inversa de A. Recordamos que con I notamos la matriz identidad de orden n.
Una matriz A cuadrada diremos que es singular si su determinante es cero; en caso contrario se dice que dicha matriz es regular (esto es, cuando el determinante es distinto de cero). Las matrices singulares no son inversibles, mientras que las regulares si lo son, por lo que hablar de matriz regular es lo mismo que hablar de matriz inversible.
Para obtener la matriz inversa de una matriz A inversible, existen varias formas entre ellas, destacamos la que utiliza la siguiente expresión:
Una matriz A cuadrada diremos que es singular si su determinante es cero; en caso contrario se dice que dicha matriz es regular (esto es, cuando el determinante es distinto de cero). Las matrices singulares no son inversibles, mientras que las regulares si lo son, por lo que hablar de matriz regular es lo mismo que hablar de matriz inversible.
Para obtener la matriz inversa de una matriz A inversible, existen varias formas entre ellas, destacamos la que utiliza la siguiente expresión:
si bien, esta expresión, para matrices de ordenes elevados y valores pequeños, lleva asociada bastante errores y por ello hay que utilizar otro tipo de métodos. tales como el método de gauss, etc.
ejemplo
Calcular, si es posible, la inversa de la siguiente matriz
Veamos primero si la matriz es inversible, es decir, su determinante es distinto de cero:
Det(A) = 3, luego es inversible.
Det(A) = 3, luego es inversible.
se calculan todos los adjuntos
por lo que la inversa resulta


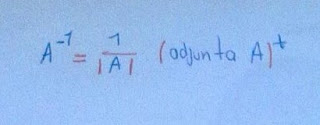




Comentarios
Publicar un comentario